El entrenamiento por potencia es una realidad en el ciclismo actual, pero a los vatios y a la famosa relación peso potencia hay que añadirle otro importante dato llamado VAM. El VAM es ese gran desconocido del ciclismo que se encarga de dictar sentencia cuando la carretera pica para arriba. Un valor tan o más determinante que el test FTP o test de 20 minutos y que muchas veces resulta menospreciado u obviado por la mayoría de preparadores físicos.
¿Qué es el VAM?
El VAM, abreviatura de Velocidad de Ascensión Media, es un invento relativamente reciente, cuyo ideólogo fue el polémico doctor Michele Ferrari, principal responsable del caso Armstrong y de la trama masiva de dopaje en el ciclismo. El VAM apareció como valor indicativo del ritmo medio de ascensión y pretendía darnos una estimación bastante precisa de la potencia relativa empleada que nos permitiera comparar ritmos entre ciclistas de diferentes características físicas.
La potencia relativa es aquella que traducida a vatios por kilo (W/kg) hace que dos ciclistas de diferente peso suban un puerto a la misma velocidad. En resumidas cuentas: Para una pendiente del 6% un ciclista de 60 kilos necesitaría apenas desarrollar 360 vatios de potencia (6w/kg) para ir igual de rápido que uno de 70 kilos con 420 vatios (6w/kg). Si la pendiente baja del 6% ganaría importancia la potencia absoluta, mientras que en caso de superarlo cobraría todavía más importancia el hecho de pesar lo menos posible. Como podéis ver y comprobar la potencia relativa permite “obviar” aparentemente un aspecto tan importante como el peso del ciclista.
El VAM nos indica el desnivel en metros positivos que es capaz de realizar un determinado ciclista en una hora y su expresión habitual se ofrece precisamente en m+/hora. Se estima que los mejores ciclistas y los escaladores puros pueden llegar a valores cercanos a los 1800 m+/h mientras que un cicloturista de nivel medio-alto difícilmente llegue a tener un VAM superior a 1200 m+/h.
Cálculo del VAM
En primer lugar decir que el cálculo del VAM nunca llegará a ser tan preciso como la de un medidor de potencia ya que la velocidad media de ascensión se ve afectada por factores externos como pueden ser el viento, el estado de la carretera, el rebufo de un coche o de otro ciclista. Dichos agentes externos distorsionan un poco la fiabilidad de interpretación del resultado pero como más exactos sean los datos que utilicemos menor será la distorsión de dicho valor.
Calcular el VAM es bastante sencillo y únicamente necesitaremos conocer el desnivel positivo de un puerto y el tiempo empleado en dicha subida. Cuando tengamos estos dos valores únicamente tendremos que dividir el desnivel positivo (en metros) entre el tiempo invertido (en horas).
Es importante que el desnivel y el tiempo sean lo más precisos posible ya que la calidad del resultado dependerá de ello.
Ejemplo:
Conseguimos ascender un puerto de 500 metros de desnivel en media hora clavada.
VAM = 500 / 0,5 = 1000 M+/h.
Bien. Hasta aquí la clase de matemáticas parece muy fácil y lógica, pero lo que realmente nos interesa es calcular la potencia relativa de cada ciclista en vatios por kilo. Aquí es dónde llega la aportación real de Ferrari ya que como hemos comentado en anterioridad es gracias a sus estimaciones que podemos calcular dicha potencia relativa sin necesidad de conocer el peso del ciclista (algo bastante complicado de saber con exactitud entre los ciclistas profesionales).

Cálculo de potencia relativa (W/kg)
Para calcular la potencia relativa en (w/kg) sin conocer el peso del ciclista Ferrari estimó la siguiente fórmula:
Potencia relativa (w/kg) = VAM (m+/h) / (Factor grado x 100)
Considerando el Factor Grado como el resultado de la siguiente expresión:
- Factor grado = 2 + (pendiente media/10)
¿La clase de física parece haberse complicado un poco más verdad? Vamos con un ejemplo.
Ejemplo:
Imaginemos que subimos el mítico Alpe D’huez (13,8km al 8,1% y con 1119 metros de desnivel positivo) con un tiempo de 57 minutos. A partir de aquí para calcular nuestra potencia relativa sería necesario obtener primero el VAM
VAM = ( 1119 / (57/60)) = 1177,,9 m/h
Una vez conocido el VAM calculamos la potencia relativa en base al factor grado:
Grado = 2 + (8,1/10) = 2,81
Potencia relativa (w/kg) = 1177,9m/h / ( 2,81x 100) = 4,1 w/kg.
Una potencia relativa de 4,1 w/kg nada desdeñable pero muy lejos de los valores y tiempos que consiguieron Marco Pantani, Lance Armstrong o Carlos Sastre en el mismo puerto. El mítico “pirata” ostenta aún el récord de la subida con un escalofriante tiempo de 36:50 minutos lo que traducido a números y a la fórmula de Ferrari sería algo tan espeluznante como:
- VAM = ( 1119/ 36,83/ 60) = 1822,9 m/h
- Potencia relativa (w/kg) = 1822,9 / ( 2,81×100) = 6,48 w/kg
Para información y análisis de este tipo os recomiendo seguir la cuenta de twitter @ammattipyoraily, que nos ofrece datos tremendamente interesantes como el siguiente acerca de los valores de los 10 primeros del tour de Francia 2014 en sus 6 mejores subidas durante la ronda gala.
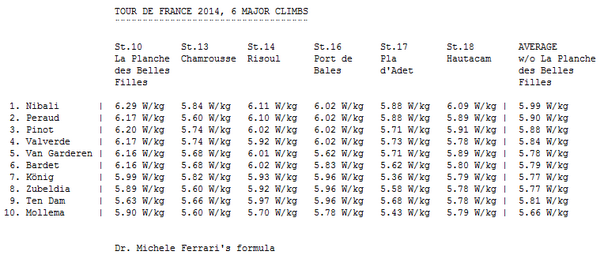
Evidentemente para conocer la potencia absoluta basta con multiplicar el resultado por el peso del ciclista.
El valor de Pantani es un valor inverosímil conseguido en 1995 tras una etapa de 200 kilómetros en plena época oscura del ciclismo y al que nadie se ha vuelto a acercar. De hecho especialistas contrastados en la materia como Antoine Vayer han llegado a dictaminar un baremo que cataloga datos por encima de los 5,8 w/kg como “no normales”, superiores a 6,14 w/kg de “milagrosos” y de más de 6,4w/kg como “mutantes”. En cualquier caso por desgracia y debido a agentes externos como el viento o el ir a rueda, dichas referencias no sirven, al menos todavía, como radar para cazar a posibles dopados. Lo que está claro y demostrado es que la física puede llegar a revelar tanto o más que la propia medicina.

























![Ideas de recetas ricas en proteína para deportistas [Consejos y ejemplos] recetas proteinas](https://www.sport.es/labolsadelcorredor/wp-content/uploads/2024/01/335195888_175794401471509_6854583834474933093_n-180x135.jpg)


![Qué es el Hyrox y cómo son las pruebas [y trucos para prepararlas] hyrox](https://www.sport.es/labolsadelcorredor/wp-content/uploads/2024/06/hyrox-barcelona-180x135.jpg)


![Correr para perder grasa abdominal: guía práctica y realista [con ejercicios] correr grasa abdominal](https://www.sport.es/labolsadelcorredor/wp-content/uploads/2024/05/correr-grasa-abdominal-180x135.jpg)














